Equivalence of PDAs and CFGs
- 使用 PDA 可以更为容易的发现 regular language 的性质
- 使用 PDA 来描述 language 更为简单,例如之前提到的合法括号序列
CFG to PDA
从L = L(G) 开始,由此来构建 N(P) = L,使得接受时为空栈
P有:
- 一个状态 q
- 输入的 symbols 是 G 的 terminal
- 栈中的 symbols 是 G 的所有 symbols 和 variables
- P 和 G 的开始状态相同
转换规则如下:
- 对于 A => a, 有(q, $\epsilon$, A) $\mapsto$ (q, a), 即将 a 压入栈中
- 对于 symbol
a有(q, a, a) $\mapsto$ (q, $\epsilon$), 即将栈顶的 a 弹出
PDA to CFG
构建 G 使得 G 与 P 等价,G 的 variable 都是形如[pXq], 指弹出栈顶 symbol X,会使得状态 p 转换为状态 q,这同时也说明了栈不会到 X 以下,如图
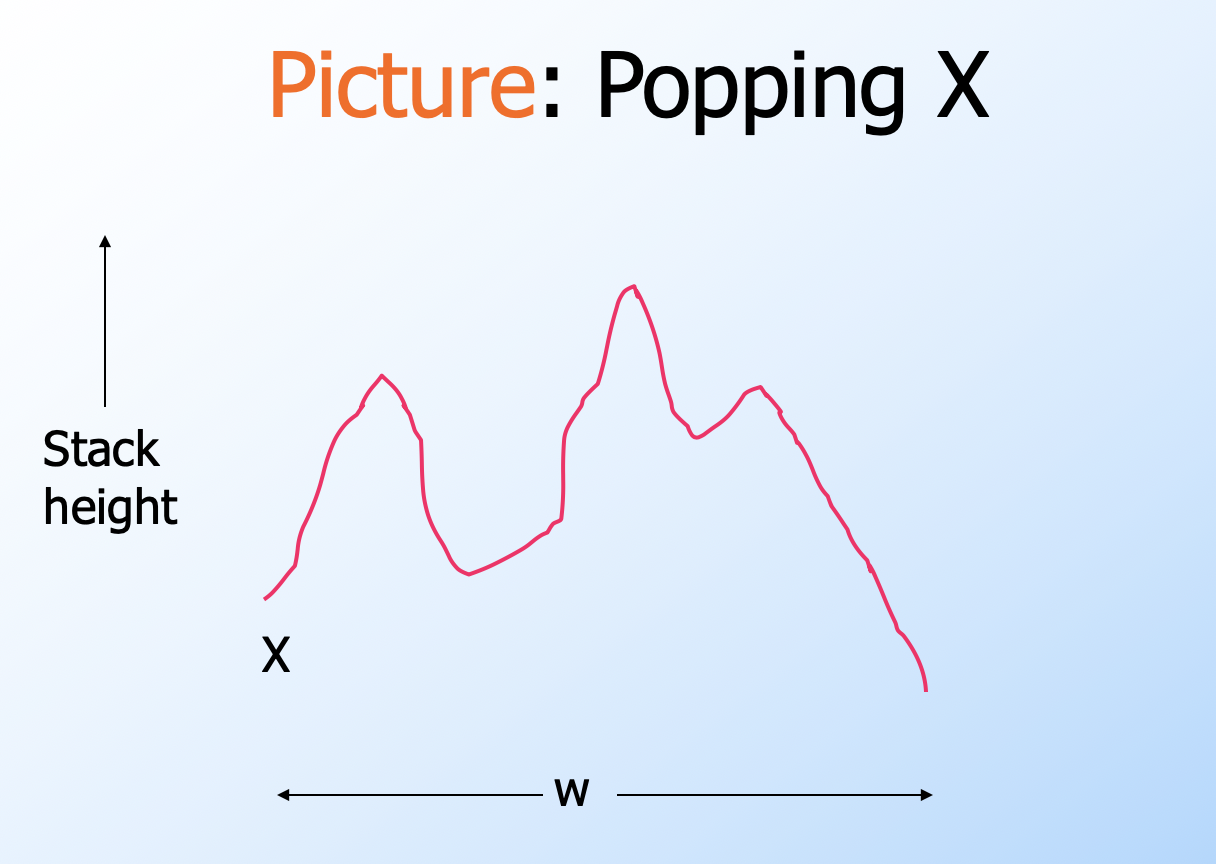
- 如果 δ(p, a, X) 包含 (q, ε),则 [pXq] -> a,,因为只有读取到 a 才能从 p 到 q 且弹出 X
- 如果 δ(p, a, X) 包含 (r, Y),则 [pXq] -> a[rYq],现在的问题已经从 p 到 q 转化为从 r 到 q,且弹出栈顶元素 Y
根据上边两条,我们可以把 δ(p, a, X) 包含 (r, Y1,…Yk),转化为 [pXq] -> a[rY1s1][s1Y2s2]…[sk-2Yk-1sk-1][sk-1Ykq]
参考
Converting a CFG to a PDA
CSCI3130: Formal Languages and Automata Theory