Introduction to context-free grammars

定义

Context-free grammar 是一个用来描述 language 的标记
相比有限自动机和 RE 更加的强大，不过仍然不能表示所有 language
对于像括号匹配和编程语言的 nested structures(?) 十分有用

Terminals = 定义的 symbol, 类似于 alphabet
Variables (aka. nonterminals) = 符号的有限集合，用来表示语言
Start symbol = 类似于 start state
Production 类似于 transition, 形如 variables(head) -> string of varibles and terminals(body)

例如: $\lbrace 0^{n}1^{n}\mid n\geq0 \rbrace$ 其中
- Terminals = $\lbrace 0,1 \rbrace$
- Variables = $\lbrace S \rbrace$
- Start symbol = S
- Productions =
  - S -> 01
  - S -> 0S1
Derivations 从 start symbol 开始，重复的使用 production 的 body 替换掉 head

在刚才的例子中，S => 0S1 => 00S11 => 000111
Iterated Derivation = =>* 就是进行0次或者更多的 derivation
Sentential Forms 从 start symbol 开始推导所得到的 form

BNF(Backus-Naur Form) Notation

编程语言的语法通常会写成 BNF

Variables 写成 <…> 如: {statement}
Terminals 通常是粗体或者是带有下划线的如 ${\bf WHILE}\ or\ \underline{WHILE}$
::= 用来代替 ->
| 用来表示或

如 S -> 0S1 | 01
… 用来表示一个或者多个

如:
{digit} ::= 0|1|2|3|4|5|6|7|8|9
{unsigned integer} ::= {digit}
条件:

{statement} ::= if {condition} then {statement} [; else {statement}]
Grouping 用 {} 来代表需要被解释为整个 unit 的 symbol

Leftmost and Rightmost Derivations

就是从左还是从右开始 derivation

$\alpha =>_{lm} \beta$ 表示 leftmost

如:
S -> SS | (S) | ()
S =>lm SS =>lm (S)S =>lm (())S =>lm (())() 就是 leftmost
S =>rm SS =>rm S() =>rm (S)() =>rm (())() 则是 rightmost

Parse tree

定义

Parse tree 就是使用 symbols 来表示的特定的 CFG(Context-free grammar)

Leaves: 树叶标记着 terminal 或者是 $\epsilon$
Interior nodes: 内部节点标记着 variable
Root: 根节点必须是 start symbol

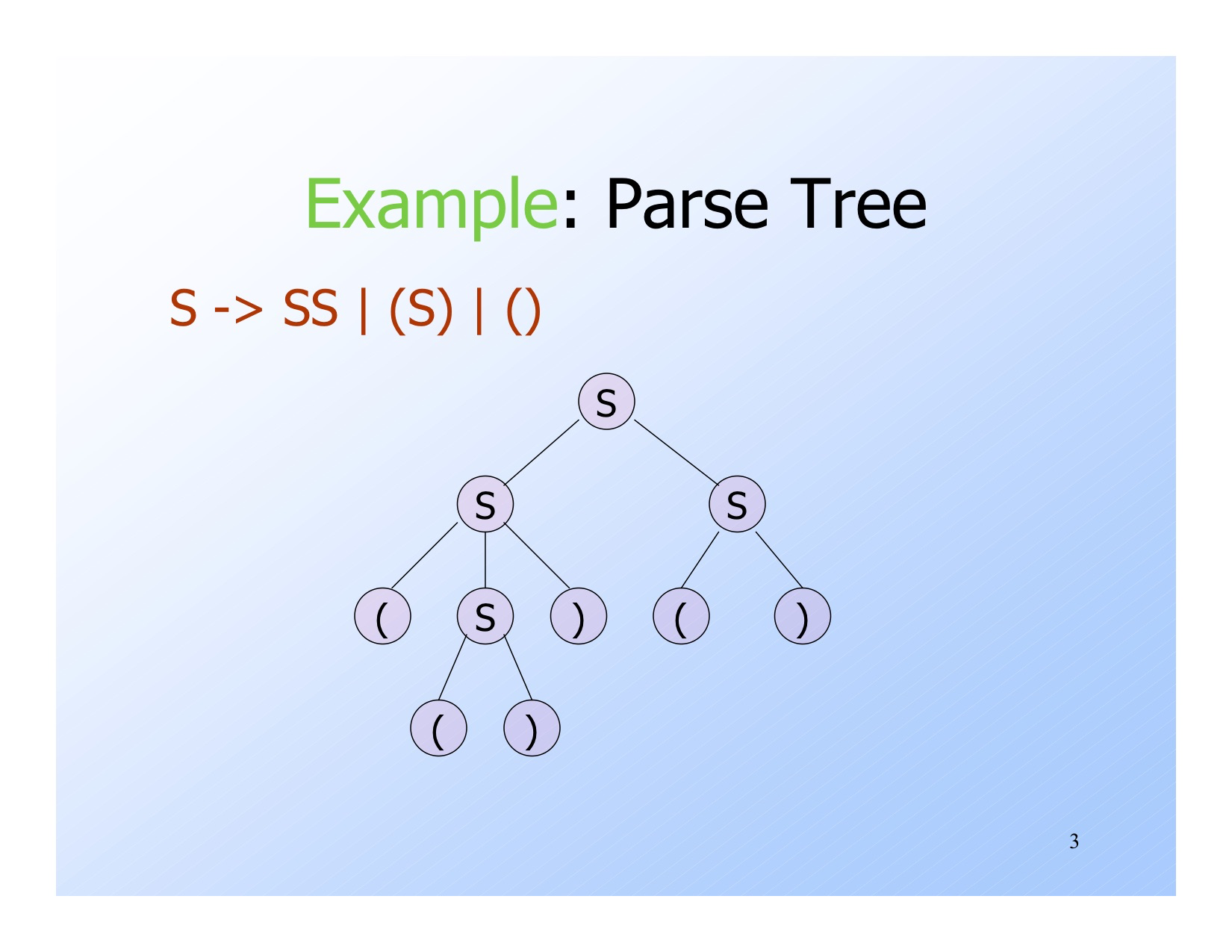
yield: 将叶子结点从左到右连接起来叫做 yield

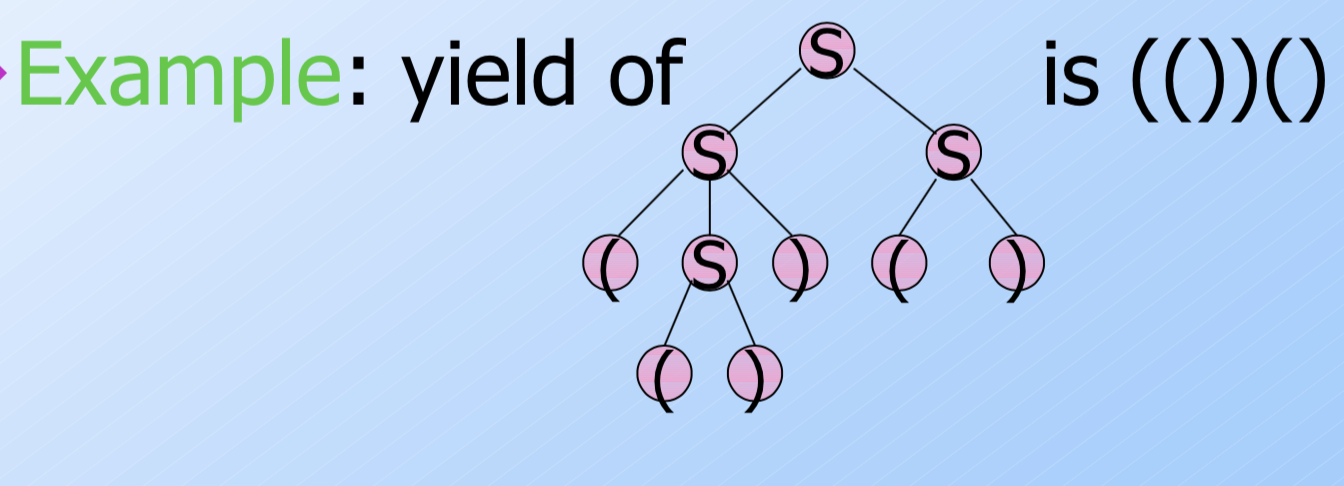
然后就是两个证明:

对于给定的 parse tree 根节点是 A 并且 yield 是 w，则 $A =>_{lm} w$
如果 $A =>_{lm} w$ 则存在一个 parse tree 且它的根节点是 A 且能够 yield w

Ambiguous Grammars

如果一个 string 可以由两个或者更多的 parse tree 所得到，那么称这个 CFG 是 ambiguous

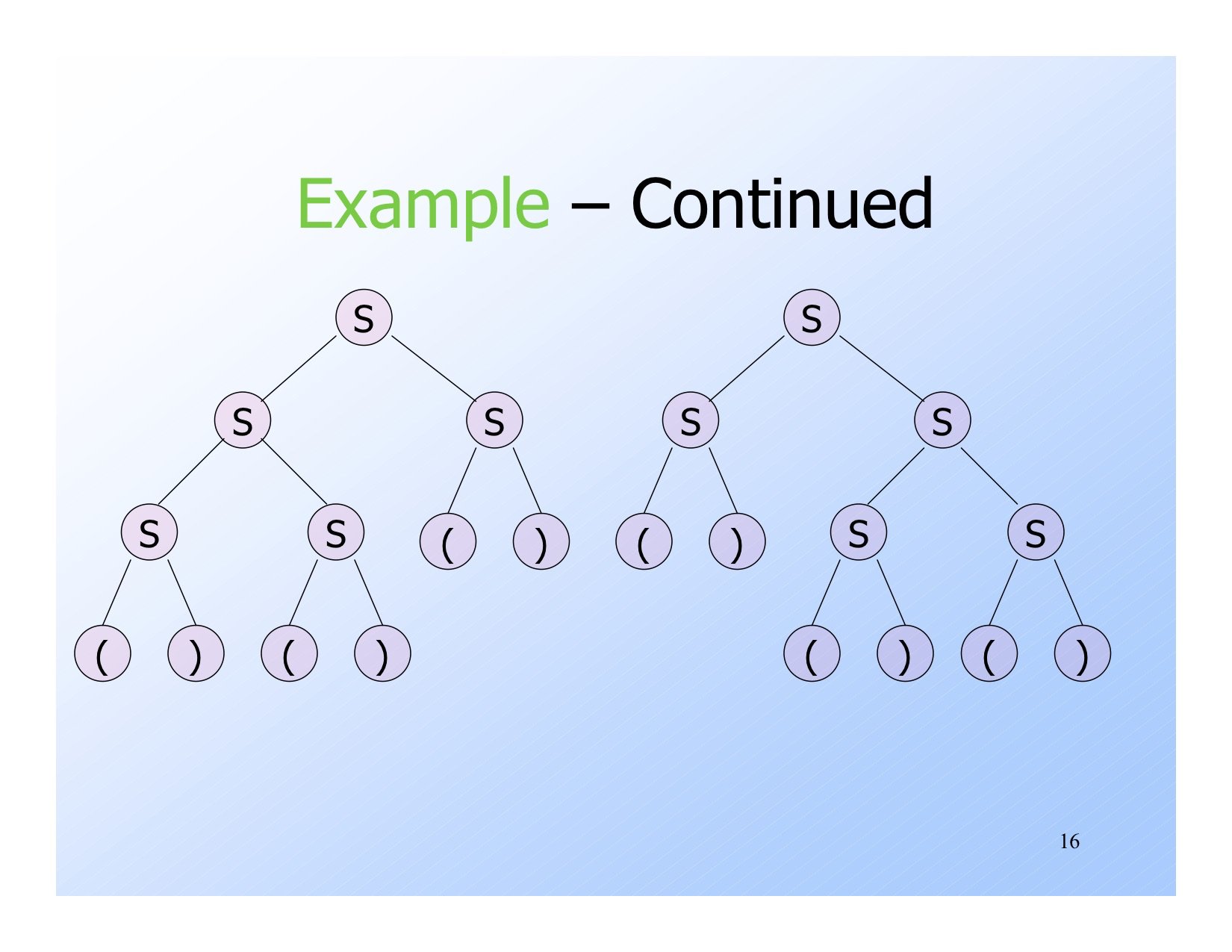
如图中的，这一个括号序列可以由两个 tree 得到

我们可以对括号序列的 grammar 进行修正

B -> (RB | ε R -> ) | (RR

需要注意的是，并不是所有的 ambiguous grammar 都可以进行修正(fix)，这些不能修正的称为 inherently ambiguous，例如 $\lbrace 0^i1^j2^k \mid i = j or j = k \rbrace$

Normal forms for context-free grammars

这一节讲的是 CFG 的正则化，就是通过一些方法来化简 CFG

Variables That Derive Nothing

定义

有些时候，variables 不能完全的转化为 terminals，比如下面的例子：

S -> AB, A -> aA|a, B -> AB
虽然 A 能够推导出 a 的所有 string，但是 B 出现了循环引用，所以 S 无法转化为只有 terminals 的状态

Algorithm to Eliminate Variables That Derive Nothing

搜索(Discovery)所有能够推导出 terminal 的 variables
去除掉所有不存在于这个集合的 production(???)

总之，最后的效果是这样的

Unreachable Symbols

所谓 unreachable symbols，就是这个 symbol 不能通过推导所到达

Eliminating Useless Symbols

useful 是能够从 start symbol 通过某种 derivation 得到特定的 terminal
否则，就是 useless

清除 Useless Symbols 需要遵循一定的顺序

Eliminate symbols that derive no terminal string
Eliminate unreachable symbols

注意这个顺序

S -> AB, A -> C, C -> c, B -> bB
如果先是去除 unreachable symbols，会发现所有的都是可以 reachable 的

Epsilon Productions

有时候我们要避免出现 A -> ε (叫做 ε-productions)的情况

Nullable Symbols

要清除 ε-productions，我们首先需要搜索 nullable symbols

S -> AB, A -> aA | ε, B -> bB | A
A 是一个 nullable，所以 B 也是
因为 S -> AB 所以 S 也是 nullable

Eliminating ε-Productions

直接上例子

S -> ABC, A -> aA | ε, B -> bB | ε, C -> ε
A, B, C 和 S 是 nullable
S -> ABC | AB | AC | BC | A | B | C
A -> aA | a
B -> bB | b

Unit Productions

unit production 就是某个 production 的 body 中只含有一个 varible

去除掉 unit productions 也比较简单

如果 A => B 且 b -> $\alpha$ 则增加一个 production A -> $\alpha$
最后扔掉其他的 production

Cleaning Up a Grammar

要清理一个 CFG，需要按照以下步骤:

Eliminate ε-productions.
Eliminate unit productions.
Eliminate variables that derive no
terminal string.
Eliminate variables not reached from the
start symbol.

注意第一步必须在前边

Chomsky Normal Form

如果一个 CFG 的 production 只有两种形式

A -> BC (2个 variables)
A -> a (1个 terminal)

那么这个 CFG 被称为 Chomsky Normal Form

Pushdown automata

PDA(Pushdown automata) 可以直观的理解为带有一个栈的 ε-NFA，不同于 NFA 的是，NFA 的转移只依赖于当前的状态和输入，而 PDA 还依赖于栈顶的元素

比如之前讨论过的 $\lbrace 0^{n}1^{n}\mid n\geq0 \rbrace$ 可以使用 PDA 来表示:

δ(q, 0, Z0) = {(q, XZ0)}
δ(q, 0, X) = {(q, XX)}
以上两条规则遇到输入为0时将 X 压入栈中
δ(q, 1, X) = {(p, ε)} 当遇到 1 时，弹出栈顶元素，并且转移到 p
δ(p, 1, X) = {(p, ε)} 遇到 1 时，出栈
δ(p, ε, Z0) = {(f, Z0)}

如果 P 是一个 PDA，

L(P) 是能够转移到末状态的 string
N(P) 是能够使栈中元素为空的 string

Steve's

Automata Week 3 笔记